In my last post, I have shown how we can define or read an array of number from a file. Having constructed the array, the question naturally arises: can we use it for something else, to do something that we could not do otherwise. The answer is yes, although in the present post, there will not be anything that I haven't discussed here or there. We have only got to put the pieces together, and with a little bit of work, we can produce three-dimensional column stacked histograms at ease. I will use the same datafile, but I repeat it here:
"" France Germany Japan Nauru
Defense 9163 4857 2648 9437
Agriculture 3547 5378 1831 1948
Education 7722 7445 731 9822
Industry 4837 147 3449 6111
"Silly walks" 3441 7297 308 7386
Then, let us see, how we are going to make that histogram! For the sake of example, we will draw four cylinders, which will be striped according to the values that the columns in the data file take. We could do two things here. Provided that we have already read the values into an array, we could draw 4 times 5 cylinders of various size and colour. Alternatively, we could draw 4 cylinders, and colour them with stripes that we take from the palette. In this case, we have to find some way of defining the proper palette. Both methods have advantages and disadvantages. The advantage of the first one is that it is faster, because the cylinders are monocolour, which means that we need only two isosamples. On the other hand, we have to have "nested" for loops (which we would just simply write out). The advantage of the second method is that we can get away with one for loop, but we need many isosamples, because the cylinders contain many colour, though the transition between the colours is required to be abrupt. But since we do not know where the boundary between two colours is, we would need many isosamples. Consequently, it will be slow.
When defining our array, we will employ the trick from the last post, and we will do something very similar, when we determine our palette. In addition, we will also have to calculate the sum in the columns, for the cylinders' height should be proportional to that. If, on the other hand, we opt for re-scaling the cylinders to the same height, we, again, need the sum. With these preliminary remarks, the first version of our script could look like this
reset
unset key
unset colorbox
unset xtics; unset xlabel
unset ytics; unset ylabel
unset ztics
file = 'marimekko.dat'
cylinder = 'cylinder.dat'
set ticslevel 0
set border 1+2+4+8
set parametric; set urange [0:2*pi]; set vrange [0:1]; set iso 2, 200
set table cylinder
splot cos(u), sin(u), v, cos(u)*v, sin(u)*v, 1
unset table
unset parametric
col = 4
row = 5
sm = 0.0
g(x,a) = (abs(x-a) < 0.1 ? 1 : 0)
h(x,a) = (x <= a ? 0.0 : 1.0)
ARRAY = "b(x, y) = 0"
SUM = "s(x,a) = 0"
PALETTE = "set palette defined (-1 0.7 0 0"
array(x, c) = (sm = h($0,0.5)*sm + x, ARRAY = ARRAY.sprintf(" + g(x,%d)*h(y,%.3f)", c, sm), \
SUM = SUM.sprintf(" + %f*g(x,%d)", x, c), x )
pal(x, c) = (PALETTE = PALETTE.sprintf(", %.1f %.3f %.3f %.3f", c-0.1, rand(0)*0.7, rand(0)*0.7, rand(0)*0.7), x
ff(x, c) = (array(x, c), x)
plot for [i=2:col+1] file every ::1 using 0:( ff(column(i), i) )
plot file every ::1 using 0:(pal(1, column(0)))
eval(ARRAY)
eval(PALETTE.")")
eval(SUM)
set xrange [4:5+3*col]
set yrange [-10:3*col-9]
splot for [i=2:col+1] cylinder using ($1+3*i):2:($3*s(i,i)):(b(i,$3*s(i,i))) with pm3d
The first couple of lines set up the graph, and they are trivial, as is the plot to the 'cylinder.dat'. The definition of g(x,a) should be familiar from the last post, and h(x,a) is nothing but the Heaviside function. We have to deal with a matrix, therefore, the string ARRAY begins with "b(x,y) = 0", which will, in due course, become the definition of a two-variable function. SUM, that will bring s(x,a) to life, also appears to define a two-variable function, but this is only apparent: s(x,a) is exactly as much of a two-variable function as is g(x,a). A mere convenience, nothing more. We also begin the definition of a palette, but we stop short of its completion: that will be done during the first plot.
In the array(x,c) function, we read in the numbers from the file, and at the same time, we also calculate the sums in the columns. This function is really similar to that from the last post. We also define a function for filling up the palette. For now, this function writes random colours into the palette at every integer.
Having defined the functions, we "plot" our data file, so as to read in the numbers. We plot the second column of the same file again, in order to prepare our palette. Note that this latter plot is really nothing but a strange way of creating a for loop: we do something as many times as there are elements in a column. In both plots, by applying the every keyword, we skip the first line, which is the column header.
At this point we are almost done: the only remaining thing is the evaluation of our new definitions, and the actual plot. The setting of the xrange and yrange is necessary only in order to ensure that the cylinders are cylinders, not elliptical.
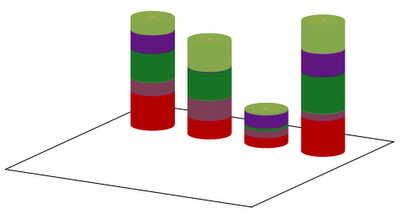
Our first script results in the graph below:
This is OK for a start, but could we improve it a bit? With some work, we could. For one thing, we could add the sum at the top of each cylinder. This can easily be done by augmenting the last plot with the line
for [i=2:col+1] file every ::0::0 using (3*i):(0):(s(i,i)+5e3):(sprintf("%d", s(i,i))) w labels
We can also give a title to each cylinder by reading out the values in the first row. This is done by adding
for [i=2:col+1] file every ::0::0 using (3*i):(-2):(0):(stringcolumn(i)) w labels centre
Finally, we can easily add a legend to the figure. All we have to do is to read out the first column of our data file, and draw 5 cylinders with the appropriate colour. We can achieve this by invoking
file using (0):(0):(2e4-$0*5e3):1 w labels right, \
for [i=1:row] cylinder using ($1+5):($2-5.0):($3*2e3+i*5e3):(i-1) with pm3d
in the last plot. With these modifications, the complete script would look like this
reset
unset key
unset colorbox
unset xtics; unset xlabel
unset ytics; unset ylabel
unset ztics
file = 'marimekko.dat'
cylinder = 'cylinder.dat'
set ticslevel 0
set border 1+2+4+8
set parametric; set urange [0:2*pi]; set vrange [0:1]; set iso 2, 200
set table cylinder
splot cos(u), sin(u), v, cos(u)*v, sin(u)*v, 1
unset table
unset parametric
col = 4
row = 5
sm = 0.0
g(x,a) = (abs(x-a) < 0.1 ? 1 : 0)
h(x,a) = (x <= a ? 0.0 : 1.0)
ARRAY = "b(x, y) = 0"
SUM = "s(x,a) = 0"
PALETTE = "set palette defined (-1 0.7 0 0"
array(x, c) = (sm = h($0,0.5)*sm + x, ARRAY = ARRAY.sprintf(" + g(x,%d)*h(y,%.3f)", c, sm), \
SUM = SUM.sprintf(" + %f*g(x,%d)", x, c), x )
pal(x, c) = (PALETTE = PALETTE.sprintf(", %.1f %.3f %.3f %.3f", c-0.1, rand(0)*0.7, rand(0)*0.7, rand(0)*0.7), x
ff(x, c) = (array(x, c), x)
plot for [i=2:col+1] file every ::1 using 0:( ff(column(i), i) )
plot file every ::1 using 0:(pal(1, column(0)))
eval(ARRAY)
eval(PALETTE.")")
eval(SUM)
set xrange [4:5+3*col]
set yrange [-10:3*col-9]
splot for [i=2:col+1] cylinder using ($1+3*i):2:($3*s(i,i)):(b(i,$3*s(i,i))) with pm3d, \
for [i=2:col+1] file every ::0::0 using (3*i):(0):(s(i,i)+5e3):(sprintf("%d", s(i,i))) w labels, \
file using (0):(0):(2e4-$0*5e3):1 w labels right, \
for [i=1:row] cylinder using ($1+5):($2-5.0):($3*2e3+i*5e3):(i-1) with pm3d, \
for [i=2:col+1] file every ::0::0 using (3*i):(-2):(0):(stringcolumn(i)) w labels centre
and would the following figure:
Well, this is sort of OK, but what if we still do not like it? There are two things that we could easily implement, and would change the character of our graph completely. One is that we can give the cylinders a true 3D lookout, by adding phongs to them. The other one is that we could remove the legends, and add it to one of the cylinders.
So, let us see what we could do in the way of phonging. This is really simple: if we think about it, the phong is nothing but a white spot on our graph, where the saturation of the colours increases towards the centre of the spot. Therefore, all we have to do is to insert white into the palette, but to do it in a way that white saturates all little cylinders. We could, then, modify our palette function as
pal(x, c) = (PALETTE = PALETTE.sprintf(", %.1f %.3f %.3f %.3f, %.1f 1 1 1", \
c-0.01, rand(0)*0.7, rand(0)*0.7, rand(0)*0.7, c+0.99), x)
and add a function that changes the saturation as
colour(x,y) = 0.25*exp(-(x-0.7)**2/0.2-(y+0.7)**2/0.2)
If we look at the palette function, the random numbers will be between 0-0.7, and the function colour(x,y) will add 0.25 to those numbers at the centre of the spot, which, in this particular case, will be at 45 degrees with respect to the x axis. When plotting, we have to add this function to our cylinders.
As for the labels, we might want to place them at the centre of each coloured cylinder in the last cylinder, representing Nauru. That is, we use the first column, and add the labels from that at half of the height of the cylinders whose size is read from the fifth column. We could use this function
lab(x) = (sm = sm + x, sm-0.5*x)
The value of sm is updated when a new value is read from the fifth column, and the return value of the function is just the cumulative sum minus half of the last value. Note that since we use sm, which was also utilised in array(x,c), we will have to re-set its value to zero before we use it.
With these modifications, the complete script reads as
reset
unset key
unset colorbox
unset xtics; unset xlabel
unset ytics; unset ylabel
unset ztics
file = 'marimekko.dat'
cylinder = 'cylinder.dat'
set ticslevel 0
set border 1+2+4+8
set parametric; set urange [0:2*pi]; set vrange [0:1]; set iso 2, 200
set table cylinder
splot cos(u), sin(u), v, cos(u)*v, sin(u)*v, 1
unset table
unset parametric
col = 4
row = 5
sm = 0.0
g(x,a) = (abs(x-a) < 0.1 ? 1 : 0)
h(x,a) = (x <= a ? 0.0 : 1.0)
ARRAY = "b(x, y) = 0"
SUM = "s(x,a) = 0"
PALETTE = "set palette defined (-1 0.7 0 0, -0.5 1 1 1"
array(x, c) = (sm = h($0,0.5)*sm + x, ARRAY = ARRAY.sprintf(" + g(x,%d)*h(y,%.3f)", c, sm), \
SUM = SUM.sprintf(" + %f*g(x,%d)", x, c), x )
pal(x, c) = (PALETTE = PALETTE.sprintf(", %.1f %.3f %.3f %.3f, %.1f 1 1 1", \
c-0.01, rand(0)*0.7, rand(0)*0.7, rand(0)*0.7, c+0.99), x)
ff(x, c) = (array(x, c), x)
colour(x,y) = 0.25*exp(-(x-0.7)**2/0.2-(y+0.7)**2/0.2)
lab(x) = (sm = sm + x, sm-0.5*x)
plot for [i=2:col+1] file every ::1 using 0:( ff(column(i), i) )
plot file every ::1 using 0:(pal(1, column(0)))
eval(ARRAY)
eval(PALETTE.")")
eval(SUM)
set xrange [4:5+3*col]
set yrange [-10:3*col-9]
splot for [i=2:col+1] cylinder using ($1+3*i):2:($3*s(i,i)):(b(i,$3*s(i,i))+colour($1,$2)) with pm3d, \
for [i=2:col+1] file every ::0::0 using (3*i):(0):(s(i,i)+5e3):(sprintf("%d", s(i,i))) w labels, \
sm = 0, file using (3*col+4):(1):(lab($5)):1 w labels left, \
for [i=2:col+1] file every ::0::0 using (3*i):(-2):(0):(stringcolumn(i)) w labels right rotate by 30

I think I cannot add more to this figure, we have explored and exhausted all possibilities here. Next time I will come back to an older topic from this blog, and show how that can be done in an elegant way, applying the new functionalities of gnuplot 4.4.
Cheers,
Zoltán